Mapping the Quantum Landscape of Electrons in Solids

SCIENTIFIC ACHIEVEMENT

Using data from the Advanced Light Source (ALS), researchers found a way to reconstruct quantum geometric tensors (QGTs)—mathematical entities that encode how an electron’s wave function is shaped by its quantum environment.

SIGNIFICANCE AND IMPACT

The mapping of QGTs enables the discovery and control of novel quantum phenomena such as superconductivity and unconventional electronic phases.

Drawing of an irregular three-dimensional surface draped over a sphere. It has a rainbow color scale, with blue at the edges and red at its peak (where it touches the top of the sphere). — The curvature of the surface where it touches the sphere depicts one aspect of an electron’s quantum landscape: the momentum-resolved effective mass of electrons in a solid. In this work, researchers established that measurements of this quantity plus the orbital angular momentum of photoemitted electrons—both accessible using angle-resolved photoemission spectroscopy (ARPES)—enable the experimental reconstruction of the QGT. The sphere is shown as a local approximation to the curvature of the surface. (Credit: Comin lab/MIT)

Toward a second quantum revolution

The development of quantum mechanics—featuring concepts such as quantized energy levels, wave-particle duality, and the uncertainty principle—revolutionized physics in the early 20th century. It led to the rise of the wave function as a way to describe, mathematically, the quantum state of a system (such as electrons in a crystal).

A more recent development, the quantum geometric tensor (QGT) is also a mathematical entity, this time describing how wave functions are affected by changes in a material’s quantum “landscape” (e.g., the material’s structure, its topological properties, electron-electron interactions, and spin-orbit coupling). The QGT is therefore a fundamental physical concept that helps explain a range of quantum phenomena in materials. However, despite its importance, a generic method for measuring the QGT in solids has been lacking.

In this work, researchers outline a way to measure the momentum-resolved QGT of solids using angle-resolved photoemission spectroscopy (ARPES). In addition to being fundamentally interesting, the QGT is also important for potential applications in next-generation microelectronics and advanced energy technologies. Studies involving the QGT will contribute immensely to what’s been dubbed the “second quantum revolution,” focusing on the control and harnessing of quantum nature at the device scale.

Introducing the quasi-QGT

Previously, the tools available for determining the QGT could only measure momentum-integrated phenomena, which are summed over all electron momenta. However, the QGT is, by definition, momentum resolved. To overcome this problem, a collaboration—primarily between theorists from Seoul National University and experimentalists from Massachusetts Institute of Technology (MIT)—introduced a quasi-QGT that is proportional to the QGT in two-band systems and an excellent approximation in multiband systems.

Like the QGT, the quasi-QGT is a complex quantity with real and imaginary parts. However, unlike the QGT, the real and imaginary parts of the quasi-QGT correspond to quantities measurable using ARPES: the momentum-resolved effective mass of electrons (i.e., the band Drude weight) for the real part, and the orbital angular momentum (OAM) of photoemitted electrons for the imaginary part.

Two flavors of ARPES

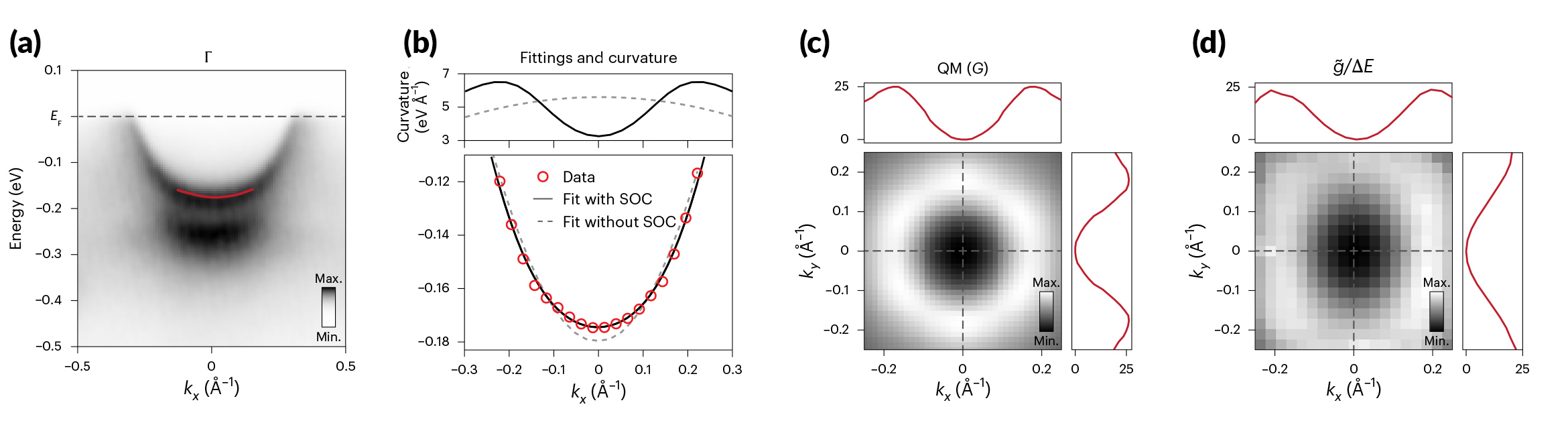
To demonstrate the viability of their approach, the researchers used high-resolution ARPES at ALS Beamline 7.0.2 (MAESTRO) to measure the band Drude weight, and they used spin-resolved circular dichroism ARPES (spin-CD-ARPES) at Elettra Synchrotron to measure the OAM. The samples consisted of cobalt tin (CoSn), a prototypical kagome metal possessing quantum geometry stemming from a topological gap at its Brillouin zone center.

At the ALS beamline, the tightly focused beam, the high-resolution electron analyzer, and the low-temperature and ultrahigh-vacuum cryostat were essential for the precise measurements needed to detect the subtle flattening of a band due to spin-orbit coupling. The change in band curvature provided data crucial to determining the real part of the quasi-QGT. With data from both the ALS and Elettra beamlines, a close correspondence between the experimental and theoretical QGT was obtained, demonstrating the efficacy of the method.

In the future, the researchers plan to apply the approach to a broad class of materials with nontrivial topology, to reveal their quantum geometry even when these effects are “hidden” (i.e., made inaccessible to other conventional probes because of the role of materials symmetries like time-reversal).

(a) Black-and-white ARPES data showing a curved (quadratic) Dirac band and a flat band below it. A red line in the Dirac band highlights its flattened curvature. (b) Dispersion of the Dirac band (as red circles) and fittings to models with and without spin-orbit coupling (black solid and grey dashed lines, respectively). (c) Plot of theoretical quantum metric. (d) Plot of experimental estimate of the quantum metric. Both (c) and (d) show dark circles surrounded by light rings, like a target bull’s-eye. — ALS ARPES data (a-b) provided a high-resolution view of the low-energy band structure of the kagome metal CoSn. This data enabled reconstruction of quantities such as (c) the quantum metric (QM)—the real part of the QGT—from experimental estimates, such as (d) g̃/ΔE, where ΔE is the energy difference between a flat band due to spin-orbit coupling (SOC) and the lower Dirac band, shown in panel (b) as the difference between solid and dotted lines.

Contact: Riccardo Comin

Researchers: M. Kang (MIT and Max Planck POSTECH/Korea Research Initiative); S. Kim, Y. Qian, J. Jung, and B.-J. Yang (Seoul National University); P.M. Neves, S. Fang, J.G. Checkelsky, and R. Comin (MIT); L. Ye (Stanford University and MIT); D. Puntel (University of Trieste, Italy); F. Mazzola (National Research Council, Italy, and Ca’ Foscari University of Venice); C. Jozwiak, A. Bostwick, and E. Rotenberg (ALS); J. Fuji and I. Vobornik (National Research Council, Italy); and J.-H. Park (Max Planck POSTECH/Korea Research Initiative and Pohang University of Science and Technology).

Funding: Air Force Office of Scientific Research; National Science Foundation; Gordon and Betty Moore Foundation; National Research Foundation of Korea; Samsung Science and Technology Foundation; Army Research Office; US Department of Energy, Office of Science, Basic Energy Sciences program (DOE BES), Center for Advancement of Topological Semimetals (an Energy Frontier Research Center led by Ames National Laboratory); Heising-Simons Physics Research Fellow Program; Tsinghua Education Foundation; Nanoscience Foundries and Fine Analysis Project, Italy; Samsung Foundation of Culture; and Kavli Institute. Operation of the ALS is supported by DOE BES.

Publication: M. Kang, S. Kim, Y. Qian, P.M. Neves, L. Ye, J. Jung, D. Puntel, F. Mazzola, S. Fang, C. Jozwiak, A. Bostwick, E. Rotenberg, J. Fuji, I. Vobornik, J.-H. Park, J.G. Checkelsky, B.-J. Yang, and R. Comin, “Measurements of the quantum geometric tensor in solids,” Nat. Phys. 21, 110 (2025), doi:10.1038/s41567-024-02678-8.

ALS SCIENCE HIGHLIGHT #519